Matrix Multiplication And Time Complexity Explained

Matrix multiplication is a fundamental operation in linear algebra and is used extensively in various fields, including physics, engineering, computer science, and data analysis. It's a crucial component in many algorithms, such as neural networks, data compression, and image processing. However, matrix multiplication can be computationally expensive, especially for large matrices. In this article, we'll delve into the world of matrix multiplication, explore its time complexity, and discuss various techniques to optimize its performance.

The Basics of Matrix Multiplication

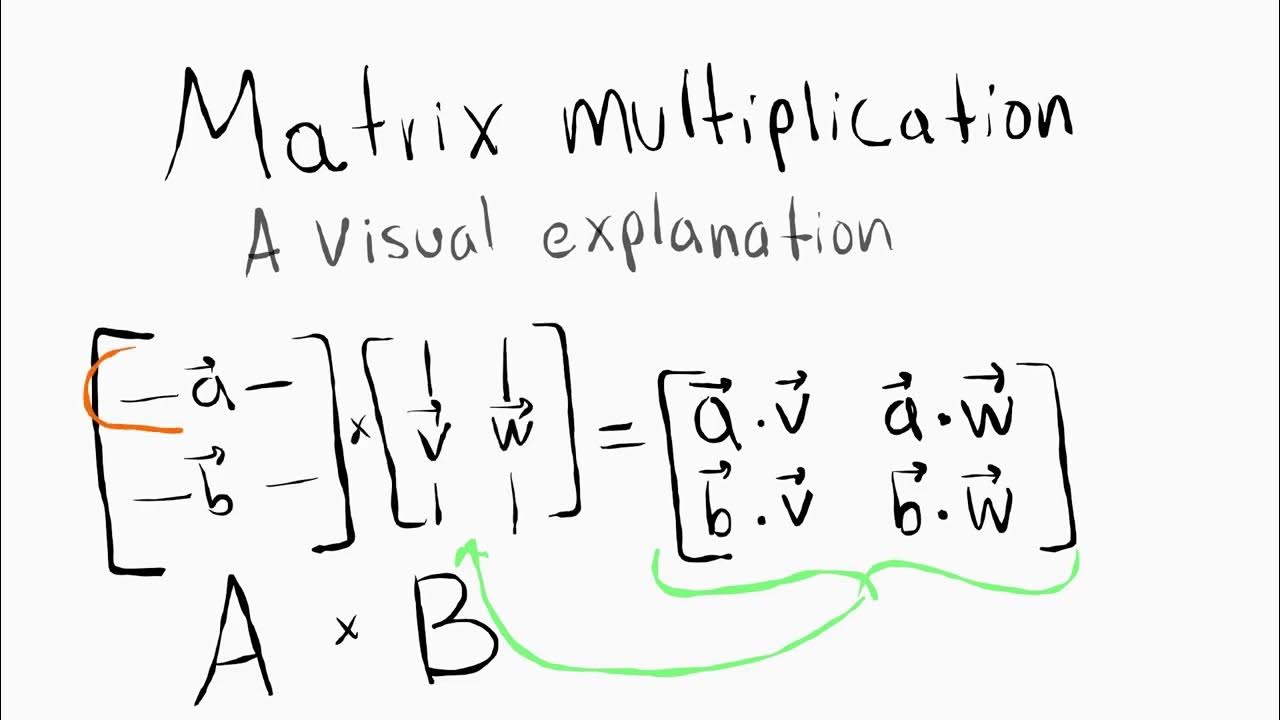
Matrix multiplication is a binary operation that takes two matrices, A and B, as input and produces another matrix, C, as output. The resulting matrix C has the same number of rows as matrix A and the same number of columns as matrix B. The elements of matrix C are calculated by multiplying the corresponding elements of rows of A with the corresponding elements of columns of B and summing the products.

For example, given two matrices A and B:

A = | 1 2 | | 3 4 |

B = | 5 6 | | 7 8 |

The resulting matrix C will be:

C = | 15 + 27 16 + 28 | | 35 + 47 36 + 48 |

C = | 19 22 | | 43 50 |

Time Complexity of Matrix Multiplication

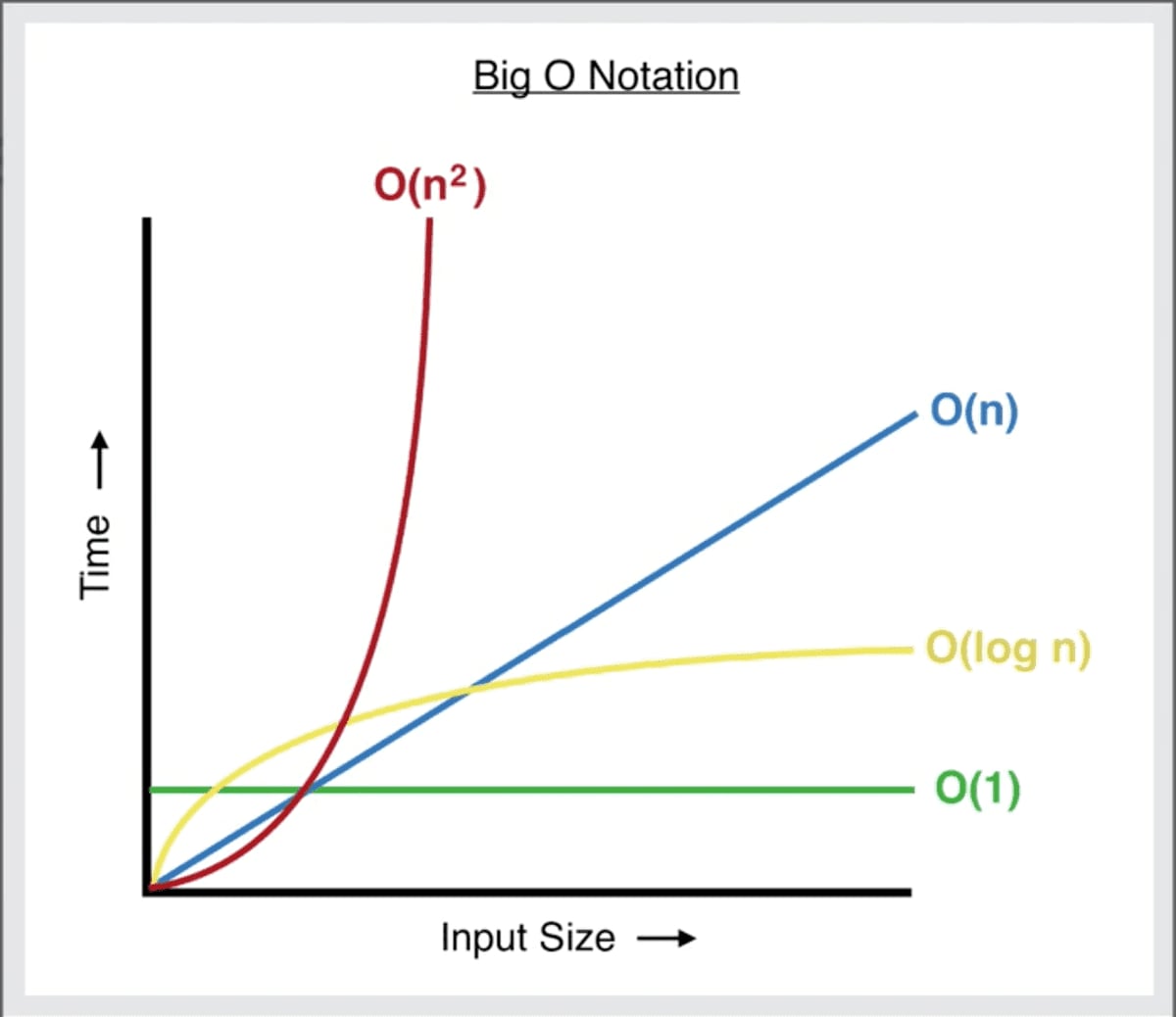
The time complexity of matrix multiplication depends on the size of the matrices and the algorithm used. The most basic algorithm for matrix multiplication has a time complexity of O(n^3), where n is the number of rows (or columns) of the matrices. This is because we need to iterate over each element of the matrices, perform a multiplication, and add the result to the corresponding element of the resulting matrix.

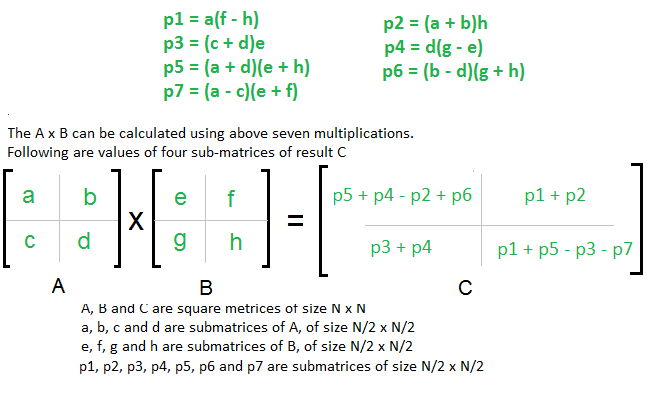
However, there are more efficient algorithms available, such as the Strassen algorithm, which has a time complexity of O(n^2.81). This algorithm uses a divide-and-conquer approach to reduce the number of multiplications required.

Optimizing Matrix Multiplication

There are several techniques to optimize matrix multiplication, including:

1. Caching: By storing frequently accessed elements in a cache, we can reduce the number of memory accesses, which can significantly improve performance.
2. Loop unrolling: By unrolling loops, we can reduce the number of iterations and improve performance.
3. Parallel processing: By dividing the matrix into smaller sub-matrices and processing them in parallel, we can take advantage of multi-core processors and improve performance.
4. Blocking: By dividing the matrix into smaller blocks and processing them separately, we can reduce the number of memory accesses and improve performance.

Techniques for Reducing Time Complexity

There are several techniques to reduce the time complexity of matrix multiplication, including:

1. Strassen algorithm: As mentioned earlier, this algorithm has a time complexity of O(n^2.81) and uses a divide-and-conquer approach to reduce the number of multiplications required.
2. Coppersmith-Winograd algorithm: This algorithm has a time complexity of O(n^2.376) and uses a combination of divide-and-conquer and fast Fourier transform techniques.
3. Fast matrix multiplication: This algorithm has a time complexity of O(n^2.25) and uses a combination of divide-and-conquer and blocking techniques.

Applications of Matrix Multiplication

Matrix multiplication has numerous applications in various fields, including:

1. Neural networks: Matrix multiplication is used extensively in neural networks to perform forward and backward passes.
2. Data compression: Matrix multiplication is used in data compression algorithms, such as JPEG and MPEG, to reduce the size of images and videos.
3. Image processing: Matrix multiplication is used in image processing algorithms, such as convolution and filtering, to perform tasks like edge detection and image segmentation.
4. Physics and engineering: Matrix multiplication is used in physics and engineering to solve systems of linear equations and perform tasks like rigid body dynamics and fluid dynamics.

Conclusion

Matrix multiplication is a fundamental operation in linear algebra and has numerous applications in various fields. However, its time complexity can be a bottleneck in many applications. By using optimized algorithms and techniques, such as caching, loop unrolling, and parallel processing, we can improve the performance of matrix multiplication. Additionally, techniques like Strassen algorithm and Coppersmith-Winograd algorithm can be used to reduce the time complexity of matrix multiplication.

What's Next?

In this article, we've explored the basics of matrix multiplication, its time complexity, and various techniques to optimize its performance. We've also discussed several applications of matrix multiplication in various fields. If you're interested in learning more about matrix multiplication and its applications, we recommend checking out the following resources:

"Matrix Multiplication" by Wikipedia "Strassen's Algorithm" by GeeksforGeeks "Coppersmith-Winograd Algorithm" by MIT OpenCourseWare

We hope you've found this article informative and helpful. If you have any questions or comments, please feel free to ask!

FAQs

Embed Image

Embed Image

Gallery of Matrix Multiplication And Time Complexity Explained