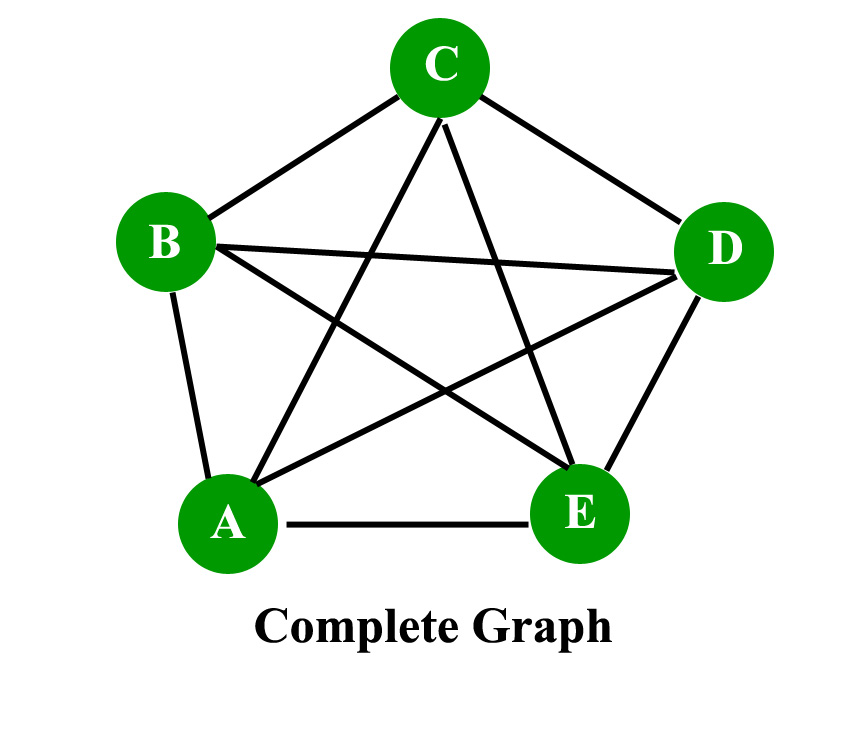
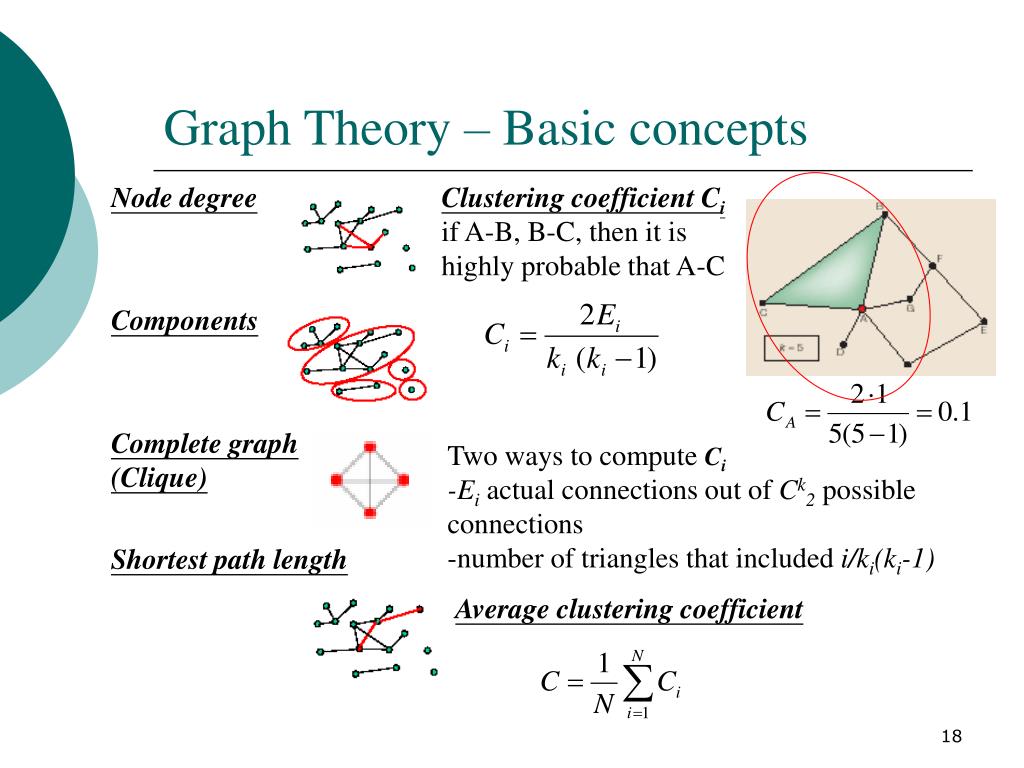
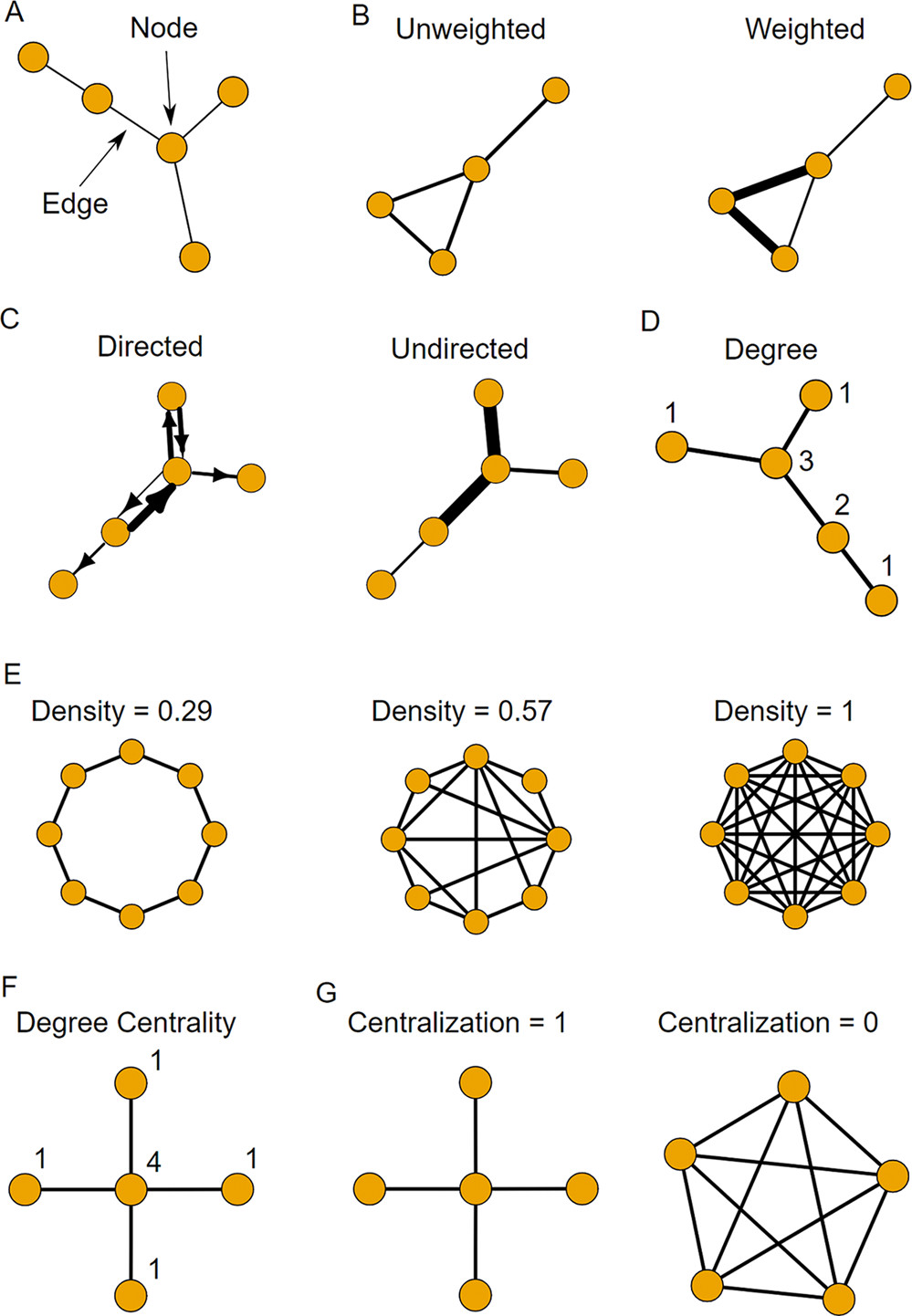
When it comes to graph theory, there are many complex concepts that can be difficult to grasp, especially for beginners. One such concept is duplication time, which is a measure of how quickly a graph can be duplicated or replicated. In this article, we will break down the concept of duplication time in graph theory, making it easy to understand for readers of all levels.
Duplication time is an important concept in graph theory, as it has many practical applications in computer science, network analysis, and other fields. It can be used to model the spread of information or disease through a network, as well as to analyze the robustness of a network to failure or attack. Despite its importance, duplication time can be a difficult concept to understand, especially for those without a strong background in graph theory.
Fortunately, with a little explanation and some simple examples, anyone can understand the basics of duplication time. So, let's dive in and explore the world of graph theory and duplication time.
What is Duplication Time in Graph Theory?
Duplication time is a measure of how quickly a graph can be duplicated or replicated. It is defined as the minimum number of steps required to create a copy of a graph, where each step consists of adding a new node or edge to the graph. The duplication time of a graph is an important concept in graph theory, as it can be used to analyze the robustness of a network to failure or attack.
For example, consider a social network where each node represents a person, and each edge represents a friendship between two people. The duplication time of this graph would represent the minimum number of steps required to create a copy of the entire social network, where each step consists of adding a new person or friendship to the network.
Types of Duplication Time
There are several types of duplication time in graph theory, including:
Node duplication time: This is the minimum number of steps required to create a copy of a graph by adding new nodes. Edge duplication time: This is the minimum number of steps required to create a copy of a graph by adding new edges. Graph duplication time: This is the minimum number of steps required to create a copy of a graph by adding new nodes and edges.
Each type of duplication time has its own unique applications and uses in graph theory.
How to Calculate Duplication Time
Calculating duplication time can be a complex task, especially for large graphs. However, there are several algorithms and techniques that can be used to calculate duplication time, including:
Breadth-first search (BFS): This algorithm can be used to calculate node duplication time by traversing the graph level by level, starting from a given node. Depth-first search (DFS): This algorithm can be used to calculate edge duplication time by traversing the graph depth by depth, starting from a given edge. Graph decomposition: This technique can be used to calculate graph duplication time by breaking down the graph into smaller subgraphs and calculating the duplication time of each subgraph.
Applications of Duplication Time
Duplication time has many practical applications in computer science, network analysis, and other fields. Some examples include:
Network robustness: Duplication time can be used to analyze the robustness of a network to failure or attack. By calculating the duplication time of a network, researchers can determine how quickly a network can be restored after a failure or attack. Information spread: Duplication time can be used to model the spread of information through a network. By calculating the duplication time of a network, researchers can determine how quickly information can spread through a network. Network design: Duplication time can be used to design networks that are robust to failure or attack. By calculating the duplication time of a network, designers can determine the minimum number of nodes and edges required to create a robust network.
Real-World Examples of Duplication Time

Duplication time has many real-world applications, including:
Social networks: Duplication time can be used to model the spread of information through social networks, such as Facebook or Twitter. Computer networks: Duplication time can be used to analyze the robustness of computer networks to failure or attack. Biological networks: Duplication time can be used to model the spread of disease through biological networks, such as the human body.
In conclusion, duplication time is an important concept in graph theory that has many practical applications in computer science, network analysis, and other fields. By understanding duplication time, researchers and designers can create robust networks that are resistant to failure or attack.
Conclusion
Duplication time is a complex concept in graph theory that can be difficult to understand, especially for beginners. However, with a little explanation and some simple examples, anyone can understand the basics of duplication time. By calculating duplication time, researchers and designers can create robust networks that are resistant to failure or attack.
We hope this article has helped you understand the concept of duplication time in graph theory. Do you have any questions or comments about duplication time? Share your thoughts in the comments section below.
FAQ Section:
What is duplication time in graph theory?
+Duplication time is a measure of how quickly a graph can be duplicated or replicated.
How is duplication time calculated?
+Duplication time can be calculated using algorithms such as breadth-first search (BFS) and depth-first search (DFS), as well as graph decomposition techniques.
What are some real-world applications of duplication time?
+Duplication time has many real-world applications, including social networks, computer networks, and biological networks.
Gallery of Understanding Duplication Time In Graph Theory Made Simple