Calculate Doubling Time In 2 Easy Steps

Calculating the doubling time of a quantity, whether it's a population, a chemical reaction, or an investment, is a crucial concept in various fields such as economics, biology, and finance. The doubling time is the period it takes for a quantity to double in size or value. In this article, we'll explore the concept of doubling time, its importance, and provide a step-by-step guide on how to calculate it in 2 easy steps.

Understanding Doubling Time

The concept of doubling time is closely related to exponential growth, where the rate of growth is proportional to the current value. In other words, as the quantity grows, the rate of growth also increases. This leads to a snowball effect, where the quantity doubles in size or value over a fixed period.

Importance of Doubling Time

Economics: to understand the growth rate of GDP, inflation, or investment returns Biology: to study population growth, chemical reactions, or the spread of diseases Finance: to calculate the growth rate of investments, such as compound interest or stock prices

Step 1: Determine the Growth Rate

To calculate the doubling time, we need to determine the growth rate of the quantity. The growth rate can be expressed as a percentage or a decimal value. The formula to calculate the growth rate is:

Growth Rate (r) = (Final Value - Initial Value) / Initial Value

For example, if the initial population is 100 and the final population is 120, the growth rate would be:

r = (120 - 100) / 100 = 0.20 or 20%

Step 2: Calculate the Doubling Time

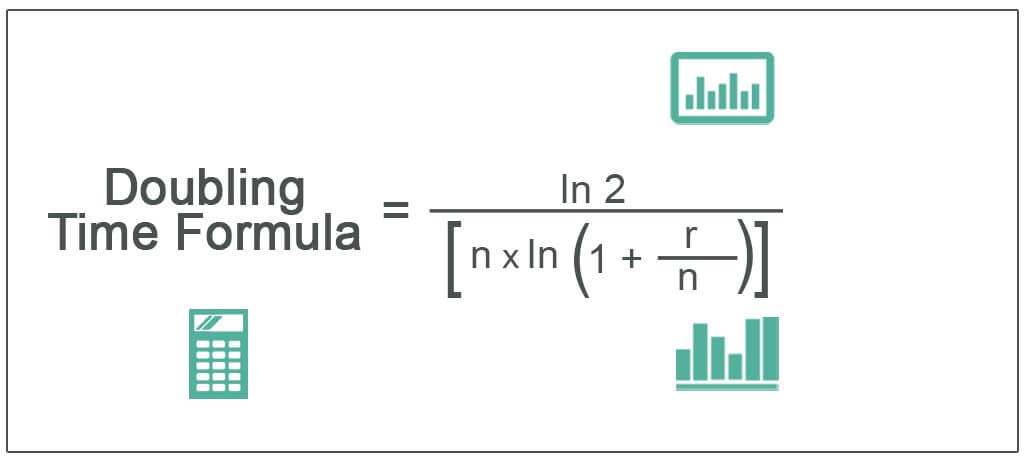
Once we have the growth rate, we can calculate the doubling time using the following formula:

Doubling Time (T) = ln(2) / ln(1 + r)

where ln is the natural logarithm.

For example, if the growth rate is 20%, the doubling time would be:

T = ln(2) / ln(1 + 0.20) = 3.8 years

This means that the population will double in size every 3.8 years.

Example Calculations

If the initial investment is $1,000 and the growth rate is 10% per annum, the doubling time would be: + Growth Rate (r) = 10% = 0.10 + Doubling Time (T) = ln(2) / ln(1 + 0.10) = 7.3 years If the initial population is 1,000 and the growth rate is 5% per annum, the doubling time would be: + Growth Rate (r) = 5% = 0.05 + Doubling Time (T) = ln(2) / ln(1 + 0.05) = 14.2 years

Conclusion and Next Steps

Calculating the doubling time is a straightforward process that requires only two steps: determining the growth rate and using the doubling time formula. By understanding the concept of doubling time, you can gain valuable insights into the growth rate of various quantities, from population growth to investment returns.

In conclusion, the doubling time is a powerful tool for analyzing exponential growth. By following these 2 easy steps, you can calculate the doubling time and gain a deeper understanding of the growth rate of various quantities. Remember to apply this concept to real-world scenarios and explore how it can be used to make informed decisions in economics, biology, and finance.

We encourage you to share your thoughts and experiences with calculating doubling time in the comments below. How do you use the concept of doubling time in your field of expertise? Share your examples and insights with our community!

Gallery of Calculate Doubling Time In 2 Easy Steps