7 Simple Multiplication Facts To Know

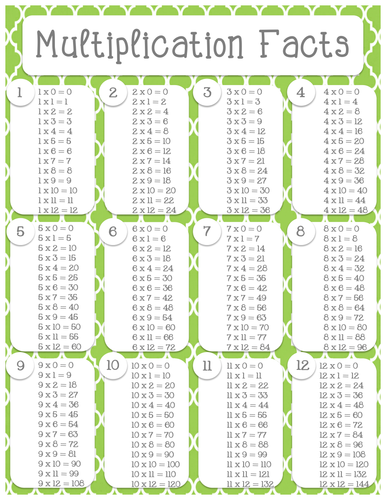
Multiplication is one of the fundamental arithmetic operations that we learn at a young age. While it may seem simple, mastering multiplication facts can be a challenging task for many students. However, with the right approach and practice, anyone can become proficient in multiplication. In this article, we will explore seven simple multiplication facts that everyone should know.

Multiplication is a vital skill that is used in various aspects of life, from cooking and shopping to finance and science. It's essential to have a solid foundation in multiplication to succeed in these areas. Moreover, understanding multiplication facts can help you to solve problems more efficiently and make calculations easier.

Mastering multiplication facts can also improve your mental math skills, which can be beneficial in everyday life. For instance, if you know that 6 × 7 = 42, you can quickly calculate the total cost of items or the area of a room without needing a calculator.

In addition to its practical applications, multiplication is also a fundamental concept in mathematics. It's used to solve algebraic equations, calculate probabilities, and understand geometric shapes. Therefore, having a strong grasp of multiplication facts is crucial for academic success in mathematics.

1. The Multiplication Tables

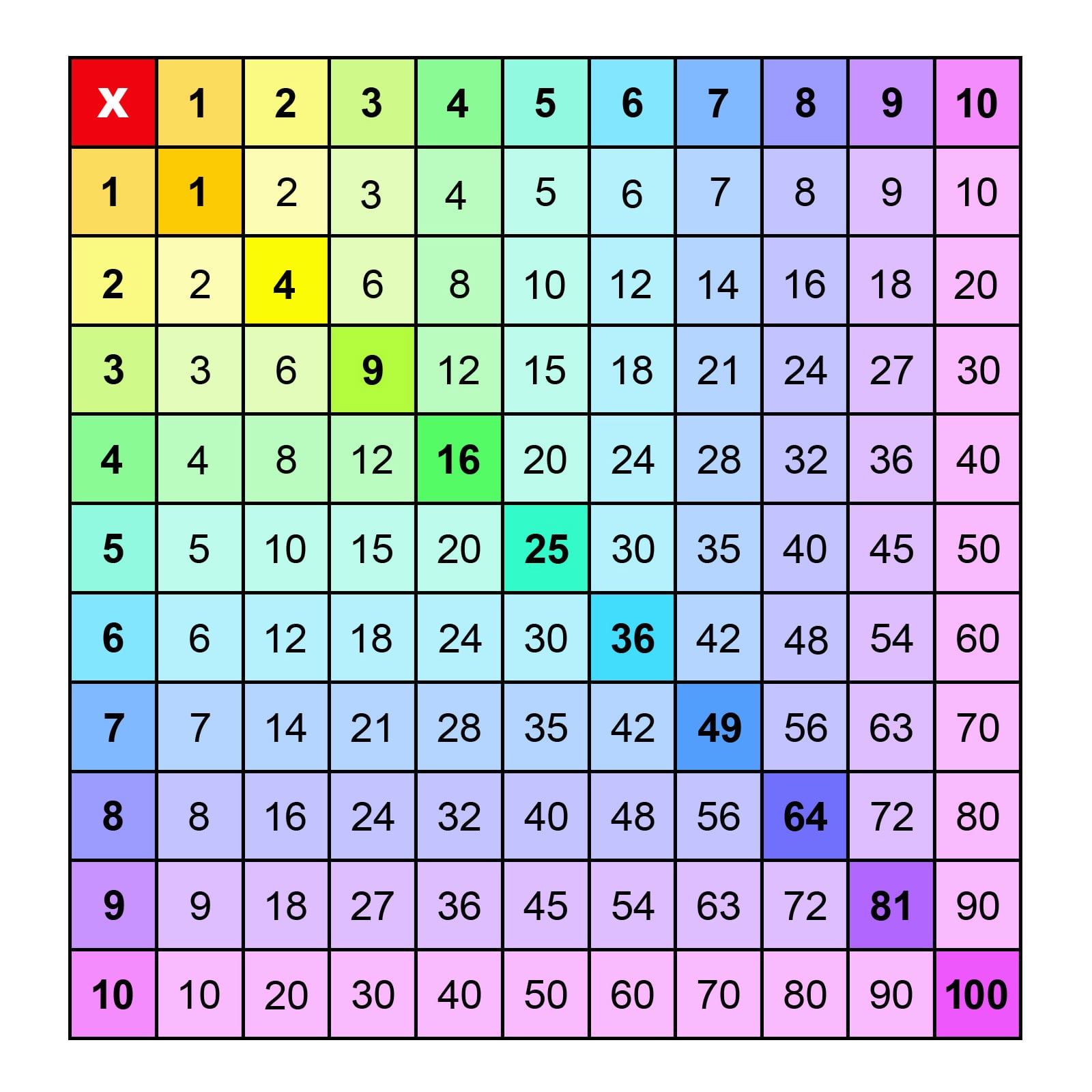
One of the simplest ways to learn multiplication facts is by memorizing the multiplication tables. The multiplication table is a grid that shows the products of numbers from 0 to 10. By memorizing the multiplication table, you can quickly recall the product of any two numbers.

For example, if you know that 4 × 5 = 20, you can use the multiplication table to calculate the product of 4 × 6. Simply look at the row for 4 and find the column for 6, and you'll see that the product is 24.

Tips for Memorizing the Multiplication Table

Start with the easy ones: Begin with the multiplication facts that are easiest to remember, such as 2 × 3 = 6 and 5 × 5 = 25. Practice regularly: Practice reciting the multiplication table regularly, either orally or in writing. Use flashcards: Create flashcards with the multiplication problem on one side and the answer on the other. Play games: Play games that involve multiplication, such as "Multiplication War" or "Multiplication Bingo."

2. The Commutative Property of Multiplication

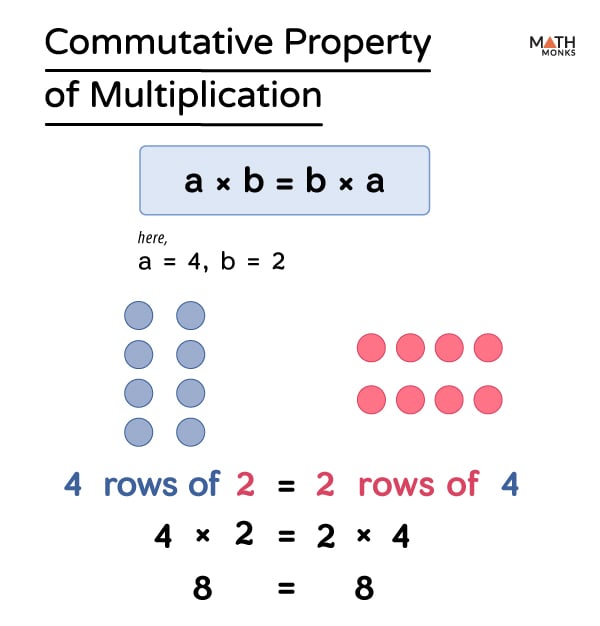
The commutative property of multiplication states that the order of the numbers being multiplied does not change the product. In other words, a × b = b × a.

For example, 2 × 3 = 3 × 2 = 6. This property can be useful when solving multiplication problems, as it allows you to change the order of the numbers to make the calculation easier.

Examples of the Commutative Property of Multiplication

2 × 3 = 3 × 2 = 6 4 × 5 = 5 × 4 = 20 6 × 7 = 7 × 6 = 42

3. The Associative Property of Multiplication

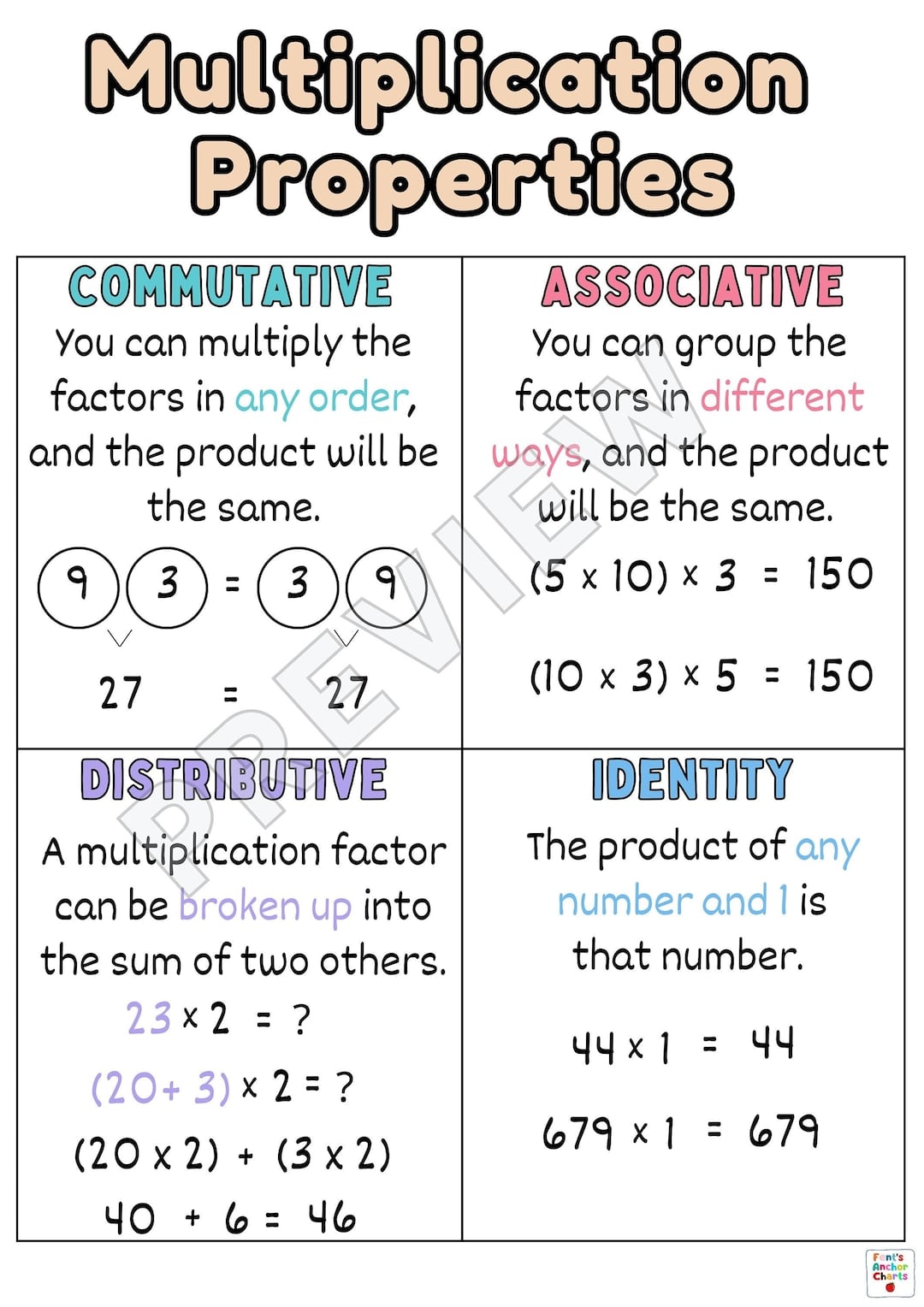
The associative property of multiplication states that when multiplying three or more numbers, the order in which you multiply them does not change the product. In other words, (a × b) × c = a × (b × c).

For example, (2 × 3) × 4 = 2 × (3 × 4) = 24. This property can be useful when solving multiplication problems that involve multiple numbers.

Examples of the Associative Property of Multiplication

(2 × 3) × 4 = 2 × (3 × 4) = 24 (4 × 5) × 6 = 4 × (5 × 6) = 120 (6 × 7) × 8 = 6 × (7 × 8) = 336

4. The Distributive Property of Multiplication

The distributive property of multiplication states that when multiplying a number by a sum or difference, you can distribute the multiplication to each term. In other words, a × (b + c) = a × b + a × c.

For example, 2 × (3 + 4) = 2 × 3 + 2 × 4 = 6 + 8 = 14. This property can be useful when solving multiplication problems that involve addition or subtraction.

Examples of the Distributive Property of Multiplication

2 × (3 + 4) = 2 × 3 + 2 × 4 = 6 + 8 = 14 4 × (5 + 6) = 4 × 5 + 4 × 6 = 20 + 24 = 44 6 × (7 + 8) = 6 × 7 + 6 × 8 = 42 + 48 = 90

5. Multiplying by Zero

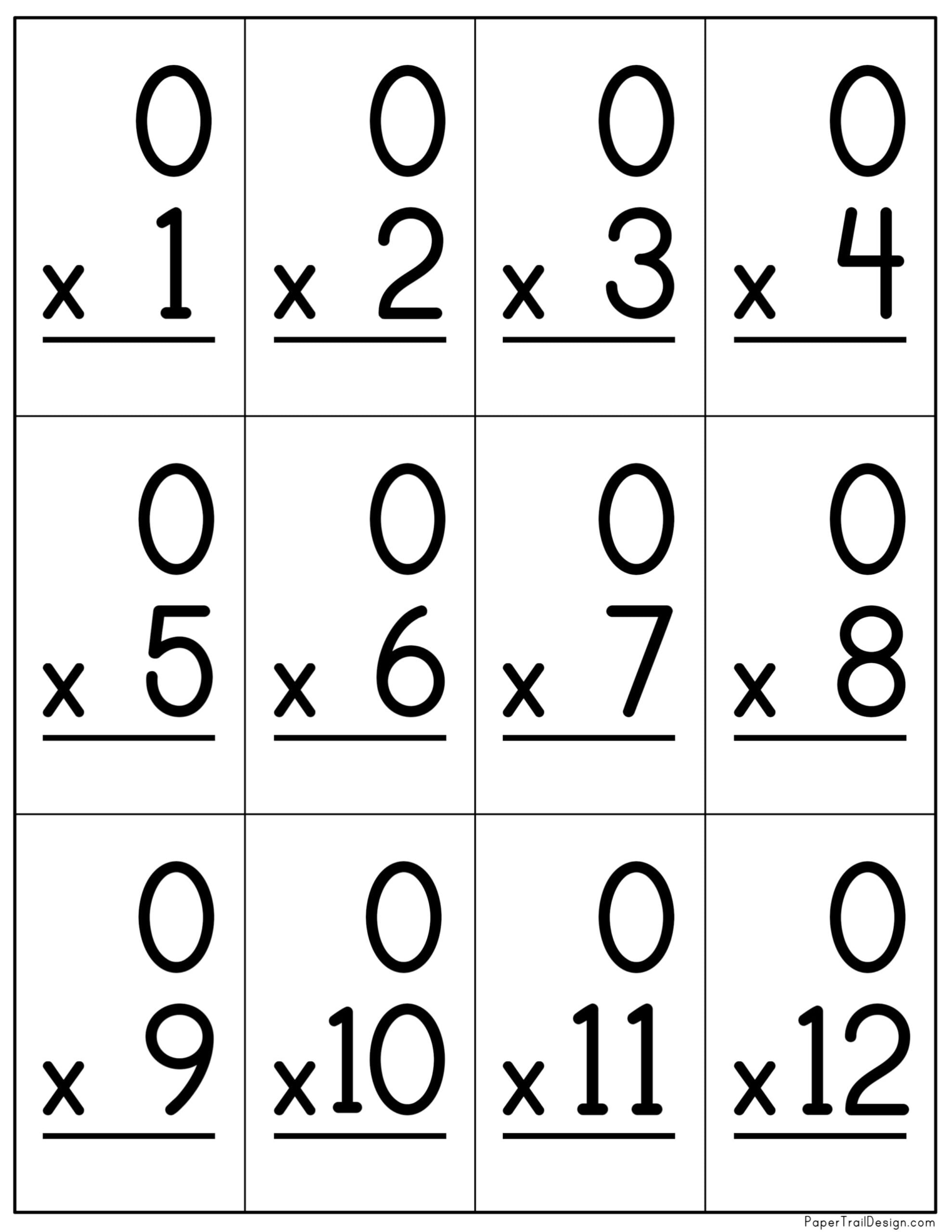
One of the simplest multiplication facts to remember is that any number multiplied by zero is equal to zero. In other words, a × 0 = 0.

For example, 2 × 0 = 0, 5 × 0 = 0, and 10 × 0 = 0. This property can be useful when solving multiplication problems that involve zero.

Examples of Multiplying by Zero

2 × 0 = 0 5 × 0 = 0 10 × 0 = 0

6. Multiplying by One

Another simple multiplication fact to remember is that any number multiplied by one is equal to itself. In other words, a × 1 = a.

For example, 2 × 1 = 2, 5 × 1 = 5, and 10 × 1 = 10. This property can be useful when solving multiplication problems that involve one.

Examples of Multiplying by One

2 × 1 = 2 5 × 1 = 5 10 × 1 = 10

7. Multiplying by Ten

Finally, one of the most useful multiplication facts to remember is that any number multiplied by ten is equal to the number with a zero added to the end. In other words, a × 10 = a0.

For example, 2 × 10 = 20, 5 × 10 = 50, and 10 × 10 = 100. This property can be useful when solving multiplication problems that involve ten.

Examples of Multiplying by Ten

2 × 10 = 20 5 × 10 = 50 10 × 10 = 100

In conclusion, mastering multiplication facts can be a challenging task, but with the right approach and practice, anyone can become proficient in multiplication. By memorizing the multiplication tables, understanding the commutative, associative, and distributive properties of multiplication, and remembering simple multiplication facts such as multiplying by zero, one, and ten, you can improve your mental math skills and solve problems more efficiently.

So, take the time to practice and review these simple multiplication facts, and you'll be well on your way to becoming a multiplication master!

Key Takeaways:

Mastering multiplication facts can improve your mental math skills and solve problems more efficiently. The commutative, associative, and distributive properties of multiplication can be useful when solving multiplication problems. Simple multiplication facts such as multiplying by zero, one, and ten can be useful when solving multiplication problems. Practice and review are key to mastering multiplication facts.

FAQs:

Share Your Thoughts:

We hope you found this article helpful in understanding the importance of multiplication facts. Do you have any favorite tips or tricks for memorizing multiplication tables? Share your thoughts in the comments below!

Take Action:

Practice and review the multiplication facts outlined in this article to improve your mental math skills and solve problems more efficiently. Try using flashcards, playing multiplication games, or solving multiplication problems online to reinforce your learning.

Gallery of 7 Simple Multiplication Facts To Know