Understanding the basics of math is essential for tackling even the simplest of calculations. One of the most fundamental concepts in mathematics is multiplication, particularly when dealing with fractions. The question of what 1/2 times 3 equals might seem straightforward, but let's break it down to ensure a solid grasp of the underlying principles.
Multiplication is essentially repeated addition. When you multiply two numbers, you're adding the first number a certain number of times, equal to the second number. However, when fractions are introduced, the concept remains the same, but the execution changes slightly.
Multiplying Fractions
Multiplying fractions involves multiplying the numerators (the numbers on top) together to get the new numerator and multiplying the denominators (the numbers on the bottom) together to get the new denominator. However, there's a simpler method when multiplying a fraction by a whole number, which is the case with 1/2 times 3.

Breaking Down 1/2 Times 3
To multiply 1/2 by 3, you essentially add 1/2 together three times.
- First, you add 1/2.
- Then, you add another 1/2.
- Finally, you add one more 1/2.
This is mathematically represented as 1/2 + 1/2 + 1/2.
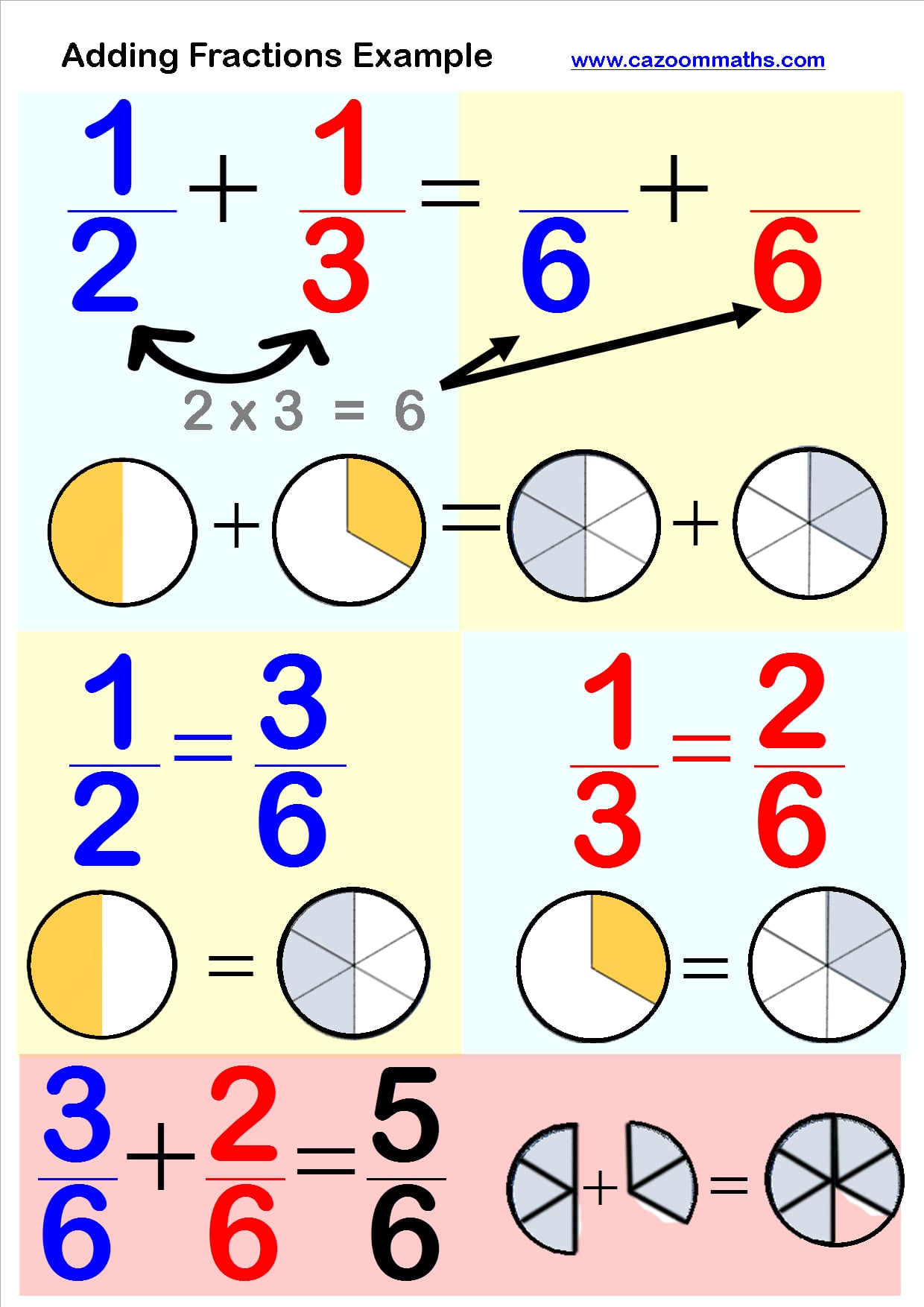
Since all three terms are the same (1/2), you can simply multiply the numerator (1) by 3, which equals 3, and keep the denominator the same (2), resulting in 3/2.
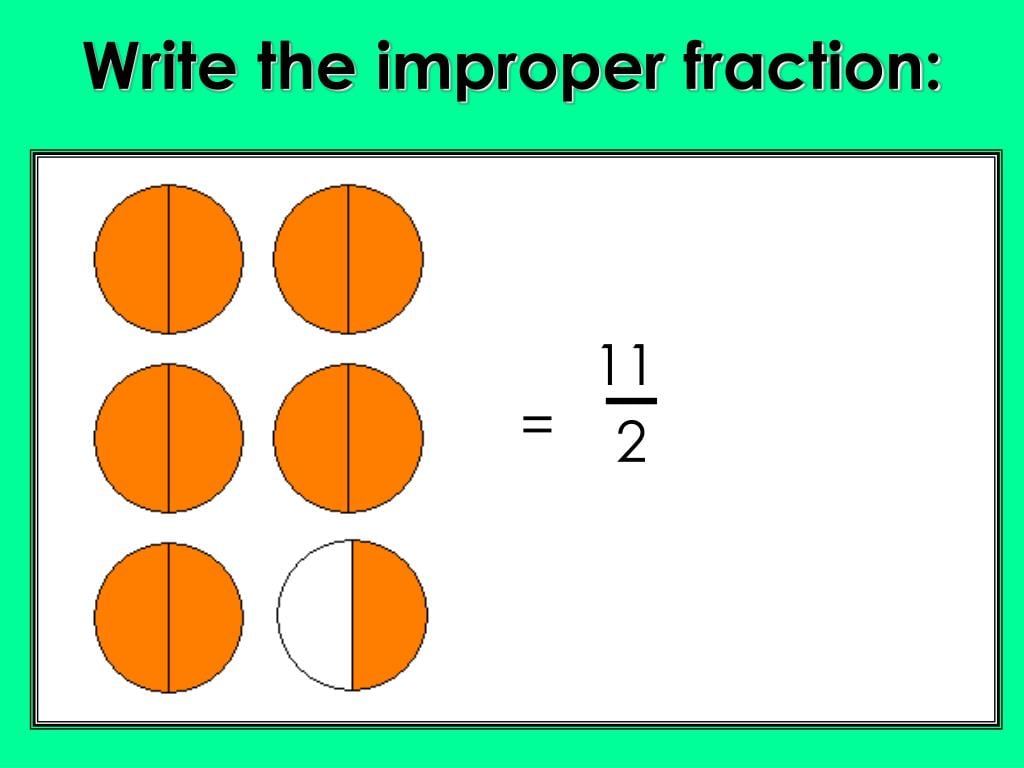
Interpreting the Result
3/2 is an improper fraction, meaning the numerator is larger than the denominator. To make it more understandable, you can convert it into a mixed number. Since 3 divided by 2 equals 1 with a remainder of 1, 3/2 can also be written as 1 1/2.
This means that the result of 1/2 times 3 is 1 and a half.
Practical Applications
Understanding how to multiply fractions is crucial in various real-world applications, such as cooking, where recipes often involve fractional amounts, and construction, where precise measurements are vital.
In cooking, multiplying fractions can help in scaling recipes up or down. For instance, if a recipe calls for 1/2 cup of flour and you need to make the recipe three times larger, understanding that 1/2 times 3 equals 1 1/2 cups can ensure your dish turns out correctly.
Conclusion: Putting It All Together
Multiplying fractions, even by whole numbers, is a straightforward process that builds upon the basic principles of multiplication and the rules of working with fractions. The example of 1/2 times 3, equaling 1 1/2, demonstrates how understanding these concepts can help in solving everyday problems with ease.
By grasping these fundamental math concepts, you're not only improving your mathematical skills but also enhancing your ability to tackle challenges in various aspects of life. Whether it's scaling a recipe, calculating areas in construction, or simply solving a math problem, knowing how to work with fractions is a powerful tool that can open doors to new possibilities.
Don't hesitate to share your thoughts or ask questions about multiplying fractions in the comments below. Sharing knowledge and experiences can be incredibly beneficial, so let's keep the conversation going!
Gallery of Easy Math: What Is 1/2 Times 3?